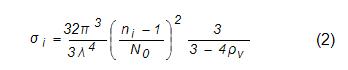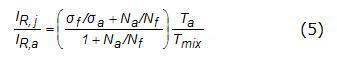Rayleigh scattering is a result of direct interaction between the incident light and the fuel molecule.
The absolute Rayleigh signal is directly proportional to the laser intensity, the total number density and the Rayleigh cross-section. In a mixture of several species, the Rayleigh signal (IR) can be represented mathematically as follows:
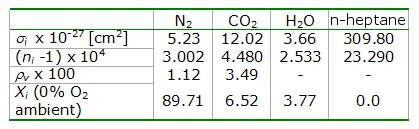
In Eq. (1), η is the signal collection efficiency, Il is the laser intensity, N is the total number density, Xi is the mole fraction and σi is the Rayleigh cross-section of species i. The Rayleigh cross-section, σi, is known for most common gases and fuels and is a function of refractive index (ni), depolarization ratio (ρv), excitation wavelength (λ) and total molecular number density at STP (N0) as shown in Eq. (2). (Values for the gases and fuel are shown in Table 4.6.1).
Table 4.6.1. Rayleigh Cross-sections, refractive index and depolarization ratio (where available) of molecules at STP and λ = 532 nm (Sutton, 2004; Fielding, 2002; Gardiner, 1981). Also shown on the last row is the ambient gas mole fraction of the inert environment (0% O2) in the constant-volume combustion vessel.
It follows from Eq. (2) that the Rayleigh cross-section, and hence the scattering efficiency, increases with decreasing excitation wavelength (λ).
In the constant-volume vessel, the diesel spray is injected into a well-characterized uniform ambient environment whose composition is known (Fig 4.6.1). Also, by injecting into an inert environment, combustion is suppressed and only the fuel vaporization process occurs.
A significant advantage of implementing the Rayleigh technique in the constant-volume combustion vessel is the ability to simultaneously measure the signal from the ambient and the jet, as shown in Fig 4.6.1. The measurement of the unmixed ambient just outside of the jet allows correction for beam steering and laser intensity distribution variation, clearly apparent in Fig 4.6.1, on a shot-by-shot basis. The ambient gases surrounding the jet consist of known constituents with known optical properties (see Table 4.6.1) and known temperature and pressure. Therefore, using Eq. (1) the Rayleigh signal from the unmixed ambient can be written as:
where, Na,o is the number density of the ambient (outside the jet) and σa is the mole-fraction weighted Rayleigh cross-section of the ambient (5.61 x 10-27 cm2). In the vapor region of the jet, the Rayleigh signal is generated by the same laser beam and from a binary mixture of the ambient and fuel vapor(Nmix=Na+Nf) (Note that Na is not the same as Na,o). Therefore, in this region Eq. (1) can be written as follows:
As Xa+Xf =1 and according to the ideal gas law Nmix/Na,o=Ta /Tmix (Ta is the ambient temperature outside the jet and Tmix is the temperature of the fuel-ambient mixture) (Espey, 1997), dividing Eq. (4) by Eq. (3) yields the following relationship:
Figure 4.6.1. The advantage of using the Rayleigh method is exhibited.
By assuming adiabatic mixing between the ambient and liquid fuel at known thermodynamic conditions, application of conservation of energy shows that Tmix = f(Na/Nf) (Espey, 1997). Therefore, one may solve for Na/Nf by utilizing this functional dependence for Tmix in Eq. (5) and measuring the Rayleigh signal from the jet and ambient (Espey, 1997).
Beam steering
A laser-intensity correction was developed that utilizes the measurement of Rayleigh scattering from the uniform ambient on both sides of the jet to account for instantaneous beam steering.
The user identifies the top and bottom jet boundary. An appropriate interpolation between the ambient values above and below the region of the jet is applied to create an instantaneous image of laser intensity variations throughout the near-uniform ambient. This image represents variations in laser intensity caused by shot-to-shot variations along the axis of the jet, as well as beam-steering-induced variations throughout the chamber. The corrected image thus obtained is the IR,a term from Eq. (5). Thus, dividing the jet image from step (5) (IR,j) by this instantaneous ‘ambient’ image (IR,a) yields Na/Nf values throughout the jet.
The ability to correct for beam-steering and shot-to-shot effects on the laser intensity distribution is a unique advantage of this Rayleigh scattering technique, when applied to a near-uniform ambient. Other laser-based techniques such as LIF also suffer from beam-steering effects. However, since the only LIF signal is from the seeded jet (ambient is not seeded and yields no signal), there is no clear way to correct for beam steering. In addition, corrections for shot-to-shot laser energy distributions are challenging for an LIF technique even when there is no beam-steering (Idicheria, 2007).